
(Source code, png)
# This serves as an intensive exercise of matplotlib's transforms
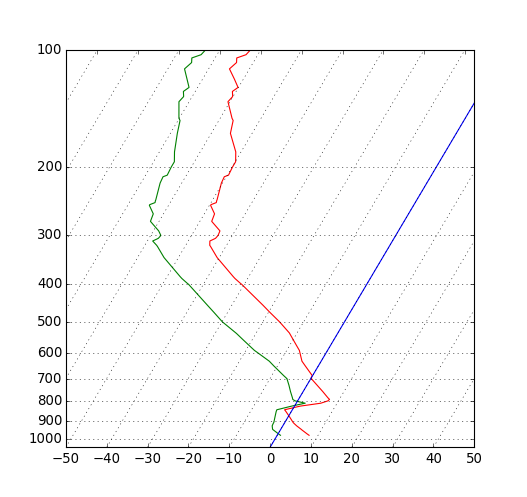
# and custom projection API. This example produces a so-called
# SkewT-logP diagram, which is a common plot in meteorology for
# displaying vertical profiles of temperature. As far as matplotlib is
# concerned, the complexity comes from having X and Y axes that are
# not orthogonal. This is handled by including a skew component to the
# basic Axes transforms. Additional complexity comes in handling the
# fact that the upper and lower X-axes have different data ranges, which
# necessitates a bunch of custom classes for ticks,spines, and the axis
# to handle this.
from matplotlib.axes import Axes
import matplotlib.transforms as transforms
import matplotlib.axis as maxis
import matplotlib.spines as mspines
import matplotlib.path as mpath
from matplotlib.projections import register_projection
# The sole purpose of this class is to look at the upper, lower, or total
# interval as appropriate and see what parts of the tick to draw, if any.
class SkewXTick(maxis.XTick):
def draw(self, renderer):
if not self.get_visible():
return
renderer.open_group(self.__name__)
lower_interval = self.axes.xaxis.lower_interval
upper_interval = self.axes.xaxis.upper_interval
if self.gridOn and transforms.interval_contains(
self.axes.xaxis.get_view_interval(), self.get_loc()):
self.gridline.draw(renderer)
if transforms.interval_contains(lower_interval, self.get_loc()):
if self.tick1On:
self.tick1line.draw(renderer)
if self.label1On:
self.label1.draw(renderer)
if transforms.interval_contains(upper_interval, self.get_loc()):
if self.tick2On:
self.tick2line.draw(renderer)
if self.label2On:
self.label2.draw(renderer)
renderer.close_group(self.__name__)
# This class exists to provide two separate sets of intervals to the tick,
# as well as create instances of the custom tick
class SkewXAxis(maxis.XAxis):
def __init__(self, *args, **kwargs):
maxis.XAxis.__init__(self, *args, **kwargs)
self.upper_interval = 0.0, 1.0
def _get_tick(self, major):
return SkewXTick(self.axes, 0, '', major=major)
@property
def lower_interval(self):
return self.axes.viewLim.intervalx
def get_view_interval(self):
return self.upper_interval[0], self.axes.viewLim.intervalx[1]
# This class exists to calculate the separate data range of the
# upper X-axis and draw the spine there. It also provides this range
# to the X-axis artist for ticking and gridlines
class SkewSpine(mspines.Spine):
def _adjust_location(self):
trans = self.axes.transDataToAxes.inverted()
if self.spine_type == 'top':
yloc = 1.0
else:
yloc = 0.0
left = trans.transform_point((0.0, yloc))[0]
right = trans.transform_point((1.0, yloc))[0]
pts = self._path.vertices
pts[0, 0] = left
pts[1, 0] = right
self.axis.upper_interval = (left, right)
# This class handles registration of the skew-xaxes as a projection as well
# as setting up the appropriate transformations. It also overrides standard
# spines and axes instances as appropriate.
class SkewXAxes(Axes):
# The projection must specify a name. This will be used be the
# user to select the projection, i.e. ``subplot(111,
# projection='skewx')``.
name = 'skewx'
def _init_axis(self):
# Taken from Axes and modified to use our modified X-axis
self.xaxis = SkewXAxis(self)
self.spines['top'].register_axis(self.xaxis)
self.spines['bottom'].register_axis(self.xaxis)
self.yaxis = maxis.YAxis(self)
self.spines['left'].register_axis(self.yaxis)
self.spines['right'].register_axis(self.yaxis)
def _gen_axes_spines(self):
spines = {'top': SkewSpine.linear_spine(self, 'top'),
'bottom': mspines.Spine.linear_spine(self, 'bottom'),
'left': mspines.Spine.linear_spine(self, 'left'),
'right': mspines.Spine.linear_spine(self, 'right')}
return spines
def _set_lim_and_transforms(self):
"""
This is called once when the plot is created to set up all the
transforms for the data, text and grids.
"""
rot = 30
# Get the standard transform setup from the Axes base class
Axes._set_lim_and_transforms(self)
# Need to put the skew in the middle, after the scale and limits,
# but before the transAxes. This way, the skew is done in Axes
# coordinates thus performing the transform around the proper origin
# We keep the pre-transAxes transform around for other users, like the
# spines for finding bounds
self.transDataToAxes = self.transScale + \
self.transLimits + transforms.Affine2D().skew_deg(rot, 0)
# Create the full transform from Data to Pixels
self.transData = self.transDataToAxes + self.transAxes
# Blended transforms like this need to have the skewing applied using
# both axes, in axes coords like before.
self._xaxis_transform = (transforms.blended_transform_factory(
self.transScale + self.transLimits,
transforms.IdentityTransform()) +
transforms.Affine2D().skew_deg(rot, 0)) + self.transAxes
# Now register the projection with matplotlib so the user can select
# it.
register_projection(SkewXAxes)
if __name__ == '__main__':
# Now make a simple example using the custom projection.
from matplotlib.ticker import ScalarFormatter, MultipleLocator
import matplotlib.pyplot as plt
from six import StringIO
import numpy as np
# Some examples data
data_txt = '''
978.0 345 7.8 0.8 61 4.16 325 14 282.7 294.6 283.4
971.0 404 7.2 0.2 61 4.01 327 17 282.7 294.2 283.4
946.7 610 5.2 -1.8 61 3.56 335 26 282.8 293.0 283.4
944.0 634 5.0 -2.0 61 3.51 336 27 282.8 292.9 283.4
925.0 798 3.4 -2.6 65 3.43 340 32 282.8 292.7 283.4
911.8 914 2.4 -2.7 69 3.46 345 37 282.9 292.9 283.5
906.0 966 2.0 -2.7 71 3.47 348 39 283.0 293.0 283.6
877.9 1219 0.4 -3.2 77 3.46 0 48 283.9 293.9 284.5
850.0 1478 -1.3 -3.7 84 3.44 0 47 284.8 294.8 285.4
841.0 1563 -1.9 -3.8 87 3.45 358 45 285.0 295.0 285.6
823.0 1736 1.4 -0.7 86 4.44 353 42 290.3 303.3 291.0
813.6 1829 4.5 1.2 80 5.17 350 40 294.5 309.8 295.4
809.0 1875 6.0 2.2 77 5.57 347 39 296.6 313.2 297.6
798.0 1988 7.4 -0.6 57 4.61 340 35 299.2 313.3 300.1
791.0 2061 7.6 -1.4 53 4.39 335 33 300.2 313.6 301.0
783.9 2134 7.0 -1.7 54 4.32 330 31 300.4 313.6 301.2
755.1 2438 4.8 -3.1 57 4.06 300 24 301.2 313.7 301.9
727.3 2743 2.5 -4.4 60 3.81 285 29 301.9 313.8 302.6
700.5 3048 0.2 -5.8 64 3.57 275 31 302.7 313.8 303.3
700.0 3054 0.2 -5.8 64 3.56 280 31 302.7 313.8 303.3
698.0 3077 0.0 -6.0 64 3.52 280 31 302.7 313.7 303.4
687.0 3204 -0.1 -7.1 59 3.28 281 31 304.0 314.3 304.6
648.9 3658 -3.2 -10.9 55 2.59 285 30 305.5 313.8 305.9
631.0 3881 -4.7 -12.7 54 2.29 289 33 306.2 313.6 306.6
600.7 4267 -6.4 -16.7 44 1.73 295 39 308.6 314.3 308.9
592.0 4381 -6.9 -17.9 41 1.59 297 41 309.3 314.6 309.6
577.6 4572 -8.1 -19.6 39 1.41 300 44 310.1 314.9 310.3
555.3 4877 -10.0 -22.3 36 1.16 295 39 311.3 315.3 311.5
536.0 5151 -11.7 -24.7 33 0.97 304 39 312.4 315.8 312.6
533.8 5182 -11.9 -25.0 33 0.95 305 39 312.5 315.8 312.7
500.0 5680 -15.9 -29.9 29 0.64 290 44 313.6 315.9 313.7
472.3 6096 -19.7 -33.4 28 0.49 285 46 314.1 315.8 314.1
453.0 6401 -22.4 -36.0 28 0.39 300 50 314.4 315.8 314.4
400.0 7310 -30.7 -43.7 27 0.20 285 44 315.0 315.8 315.0
399.7 7315 -30.8 -43.8 27 0.20 285 44 315.0 315.8 315.0
387.0 7543 -33.1 -46.1 26 0.16 281 47 314.9 315.5 314.9
382.7 7620 -33.8 -46.8 26 0.15 280 48 315.0 315.6 315.0
342.0 8398 -40.5 -53.5 23 0.08 293 52 316.1 316.4 316.1
320.4 8839 -43.7 -56.7 22 0.06 300 54 317.6 317.8 317.6
318.0 8890 -44.1 -57.1 22 0.05 301 55 317.8 318.0 317.8
310.0 9060 -44.7 -58.7 19 0.04 304 61 319.2 319.4 319.2
306.1 9144 -43.9 -57.9 20 0.05 305 63 321.5 321.7 321.5
305.0 9169 -43.7 -57.7 20 0.05 303 63 322.1 322.4 322.1
300.0 9280 -43.5 -57.5 20 0.05 295 64 323.9 324.2 323.9
292.0 9462 -43.7 -58.7 17 0.05 293 67 326.2 326.4 326.2
276.0 9838 -47.1 -62.1 16 0.03 290 74 326.6 326.7 326.6
264.0 10132 -47.5 -62.5 16 0.03 288 79 330.1 330.3 330.1
251.0 10464 -49.7 -64.7 16 0.03 285 85 331.7 331.8 331.7
250.0 10490 -49.7 -64.7 16 0.03 285 85 332.1 332.2 332.1
247.0 10569 -48.7 -63.7 16 0.03 283 88 334.7 334.8 334.7
244.0 10649 -48.9 -63.9 16 0.03 280 91 335.6 335.7 335.6
243.3 10668 -48.9 -63.9 16 0.03 280 91 335.8 335.9 335.8
220.0 11327 -50.3 -65.3 15 0.03 280 85 343.5 343.6 343.5
212.0 11569 -50.5 -65.5 15 0.03 280 83 346.8 346.9 346.8
210.0 11631 -49.7 -64.7 16 0.03 280 83 349.0 349.1 349.0
200.0 11950 -49.9 -64.9 15 0.03 280 80 353.6 353.7 353.6
194.0 12149 -49.9 -64.9 15 0.03 279 78 356.7 356.8 356.7
183.0 12529 -51.3 -66.3 15 0.03 278 75 360.4 360.5 360.4
164.0 13233 -55.3 -68.3 18 0.02 277 69 365.2 365.3 365.2
152.0 13716 -56.5 -69.5 18 0.02 275 65 371.1 371.2 371.1
150.0 13800 -57.1 -70.1 18 0.02 275 64 371.5 371.6 371.5
136.0 14414 -60.5 -72.5 19 0.02 268 54 376.0 376.1 376.0
132.0 14600 -60.1 -72.1 19 0.02 265 51 380.0 380.1 380.0
131.4 14630 -60.2 -72.2 19 0.02 265 51 380.3 380.4 380.3
128.0 14792 -60.9 -72.9 19 0.02 266 50 381.9 382.0 381.9
125.0 14939 -60.1 -72.1 19 0.02 268 49 385.9 386.0 385.9
119.0 15240 -62.2 -73.8 20 0.01 270 48 387.4 387.5 387.4
112.0 15616 -64.9 -75.9 21 0.01 265 53 389.3 389.3 389.3
108.0 15838 -64.1 -75.1 21 0.01 265 58 394.8 394.9 394.8
107.8 15850 -64.1 -75.1 21 0.01 265 58 395.0 395.1 395.0
105.0 16010 -64.7 -75.7 21 0.01 272 50 396.9 396.9 396.9
103.0 16128 -62.9 -73.9 21 0.02 277 45 402.5 402.6 402.5
100.0 16310 -62.5 -73.5 21 0.02 285 36 406.7 406.8 406.7
'''
# Parse the data
sound_data = StringIO(data_txt)
p, h, T, Td = np.loadtxt(sound_data, usecols=range(0, 4), unpack=True)
# Create a new figure. The dimensions here give a good aspect ratio
fig = plt.figure(figsize=(6.5875, 6.2125))
ax = fig.add_subplot(111, projection='skewx')
plt.grid(True)
# Plot the data using normal plotting functions, in this case using
# log scaling in Y, as dicatated by the typical meteorological plot
ax.semilogy(T, p, 'r')
ax.semilogy(Td, p, 'g')
# An example of a slanted line at constant X
l = ax.axvline(0, color='b')
# Disables the log-formatting that comes with semilogy
ax.yaxis.set_major_formatter(ScalarFormatter())
ax.set_yticks(np.linspace(100, 1000, 10))
ax.set_ylim(1050, 100)
ax.xaxis.set_major_locator(MultipleLocator(10))
ax.set_xlim(-50, 50)
plt.show()
Keywords: python, matplotlib, pylab, example, codex (see Search examples)